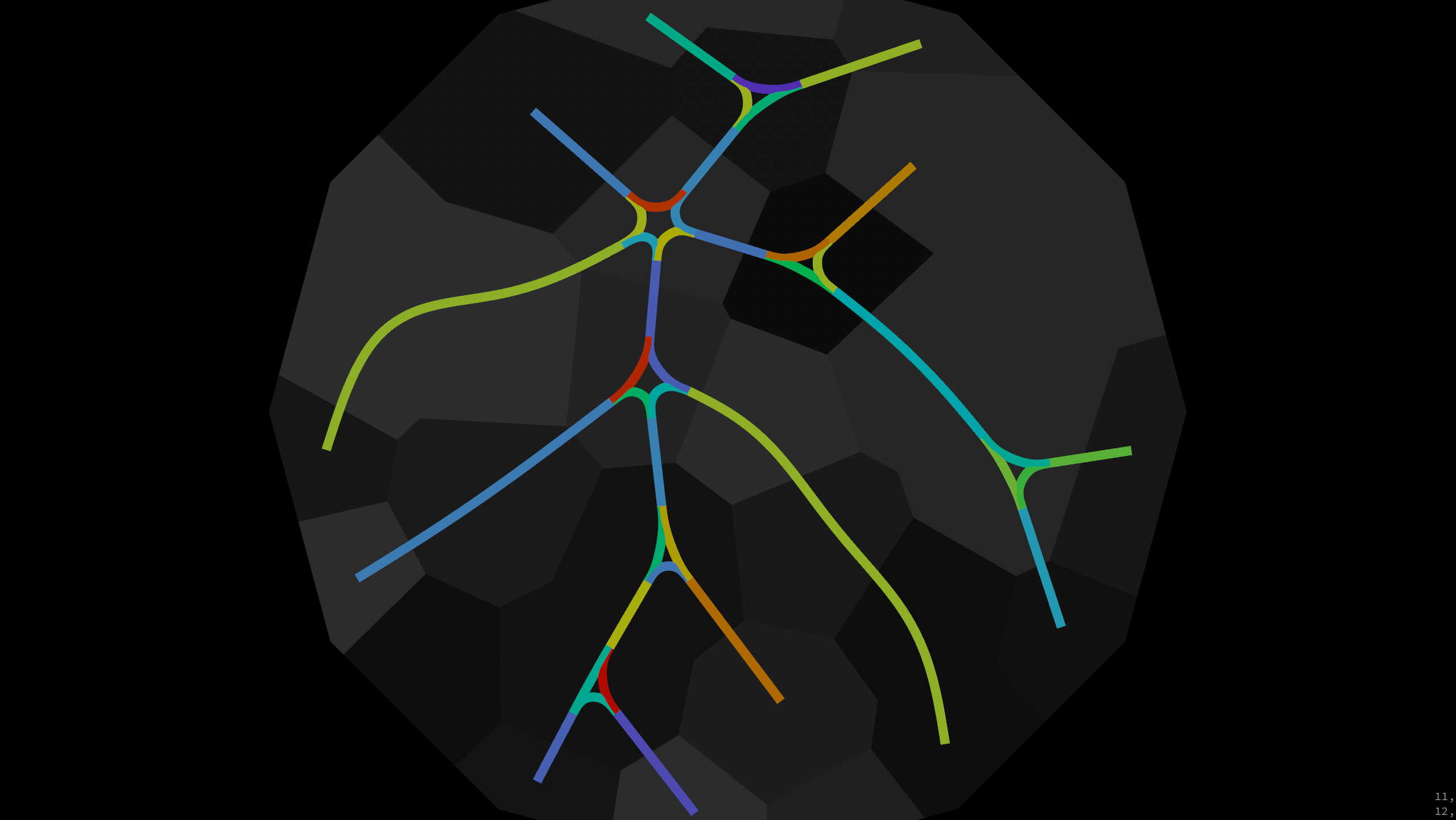

Dual voronoi network with shortest paths and curved crossings.
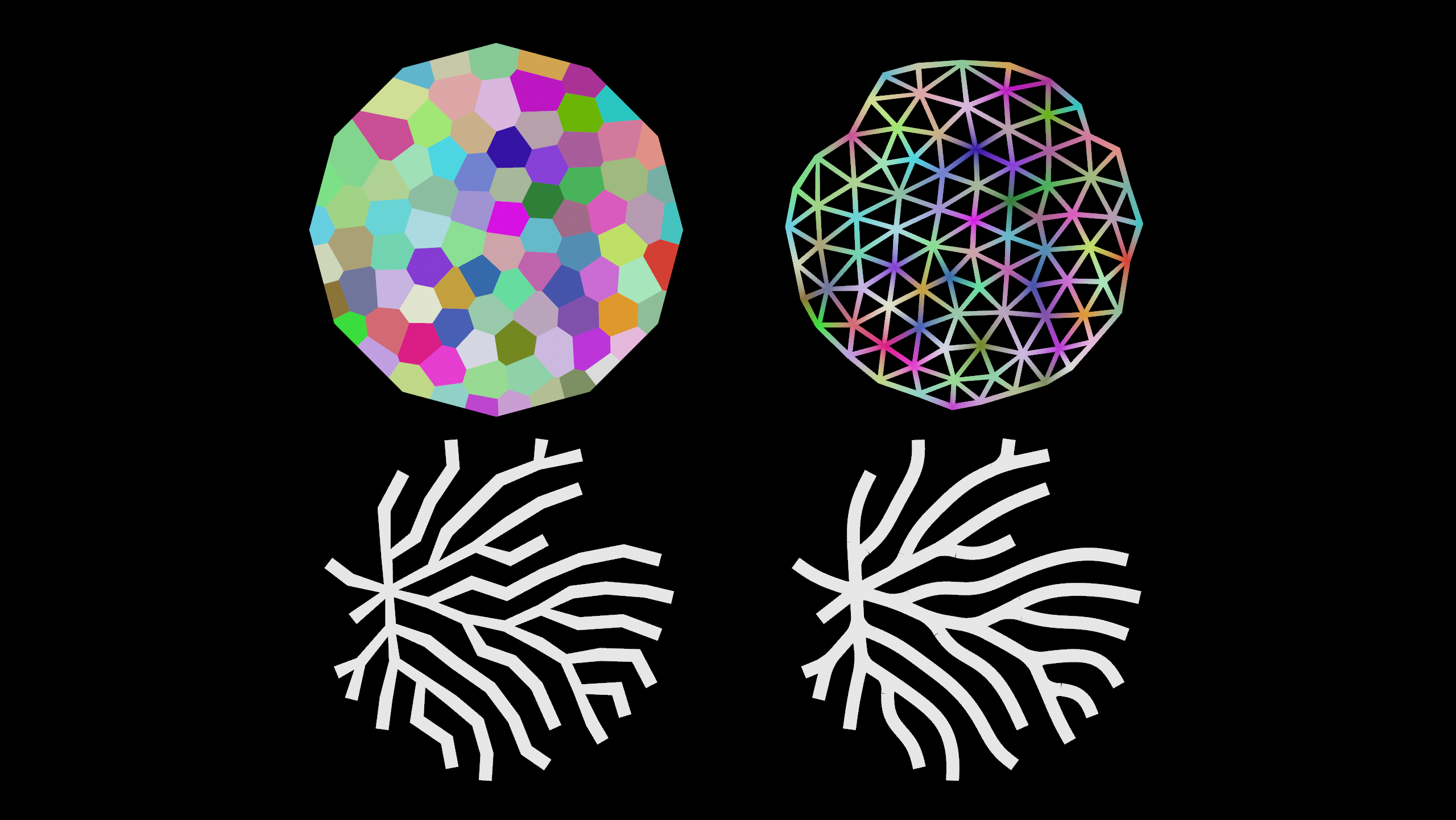
First we identify crossings by the number of neighbour points.
neighbourcount(0, i@ptnum)>2
We set up an array nbs[] of neighbour points. In the first loop we calculate their angle in relation to their center to order the neighbour points counter-clockwise with argsort and reorder.
The second loop calculates intermediate points located halfway between a neighbour and the center point (point(0, 'P', nb) + v@P) / 2.0. The third loop connects consecutive neighbour points along with one intermediate point to a curve.
int nbs[] = neighbours(0, i@ptnum);
float angle[];
foreach(int nb; nbs){
vector pos = point(0, 'P', nb) - v@P;
float a = atan(pos.x, pos.z);
append(angle, a);
}
int indices[] = argsort(angle);
nbs = reorder(nbs, indices);
int pts[];
foreach(int nb; nbs){
vector pos_pt = (point(0, 'P', nb) + v@P) / 2.0;
int pt = addpoint(0, pos_pt);
append(pts, pt);
}
foreach(int i; int nb; nbs){
int pt_next = nbs[(i+1)%len(nbs)];
int pr = addprim(0, 'polyline', nb, pts[i], pts[(i+1)%len(pts)], pt_next);
setprimgroup(0, 'crossing', pr, 1, 'set');
}
removepoint(0, i@ptnum);