Making a grid flow through guide points using multivariate interpolation with the Python module Numpy / Scipy.
The f@height attribute is going to be interpolated based on common X and Z positions between the grid and the guide points.
// Grid
f@px = v@P.x;
f@pz = v@P.z;
f@height = 0.0;
// Guide points
f@px = v@P.x;
f@pz = v@P.z;
f@height = v@P.y;
Python's NumPy/SciPy library offers multivariate interpolation. It's making sure the grid will always flow smoothly through our guide points even if they are positioned irregularily.
There are various interpolation methodes provided: multiquadric, inverse multiquadric, gaussian, linear, cubic, quintic and thinplate.
import numpy as np
from scipy.interpolate import griddata
import scipy.interpolate as interp
node = hou.pwd()
geo1 = node.geometry()
inputs = node.inputs()
geo2 = inputs[1].geometry()
method_nr = node.evalParm('method')
method_names = 'multiquadric,inverse_multiquadric,gaussian,linear,cubic,quintic,thin_plate'.split(',')
method_str = method_names[method_nr]
grid_x = np.array(geo1.pointFloatAttribValues('px'))
grid_z = np.array(geo1.pointFloatAttribValues('pz'))
pos_x = np.array(geo2.pointFloatAttribValues('px'))
pos_z = np.array(geo2.pointFloatAttribValues('pz'))
height = np.array(geo2.pointFloatAttribValues('height'))
rbf_height = interp.Rbf(pos_x, pos_z, height, function=method_str)
smooth_rbf_height = rbf_height(grid_x, grid_z)
geo1.setPointFloatAttribValuesFromString("height", smooth_rbf_height.astype(np.float32))
v@P.y = f@height;
The radial basis function (RBF) in Scipy.interpolate does an excellent job at interpolating between irregular points. RBF looks smoother than what we´d get from the Attribute Transfer SOP, too.
Adrian Pan contributed a corresponding example file that works directly with heightfields.
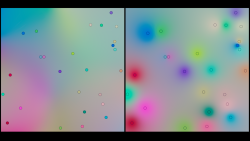
rbf.hip contains a simplified VEX version of multivariate interpolation using radial basis functions. The screenshot compares the attribute transfer node's result (left) with RBF.
float shape = chf('shape');
float power = chf('power');
vector positions[] = detail(1, 'pos', 0);
vector pos = {0.0, 0.0, 0.0};
float weight = 0.0;
foreach(vector p; positions){
float d = distance2(v@P, p);
float w = exp(-d / (2.0 * pow(shape, power)));
pos += p * w;
weight += w;
}
v@P = pos /= weight;
12
Programming
172
Programming
25
Programming
204
ProgrammingRendering
269
AutomationProgramming
258
ModelingProgramming
