

A collection of VEX functions useful for procedural modeling.

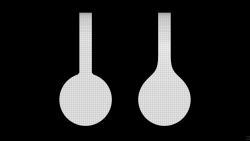
Creates shapes based on u, eg. the curveu attribute from the resample node, or a component of the UV coordinates from the sweep node.
Recommended values: center 0.5; weight <= 0.5; power > 0.0; amount > 0.0.
float center = chf('center');
float weight = chf('weight');
float power = chf('power');
float amount = chf('amount');
function float shape(float c, w, p, a, u){
u = abs(u - c);
if(u > w) return 0.0;
u /= w;
float d = 1.0 - u * u * (3.0 - 2.0 * u);
d = pow(d, p) * a;
return d;
}
float u = vertexprimindex(0, i@vtxnum) / (primvertexcount(0, i@primnum) - 1.0);
v@P.y = shape(center, weight, power, amount, u);
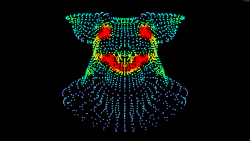
Calculates the smooth k minimum of two distances a and b.
function float smooth_min(float a, b, k){
float h = max(k - abs(a - b), 0.0) / k;
float d = min(a, b) - h * h * h * k * (1.0 / 6.0);
return d;
}
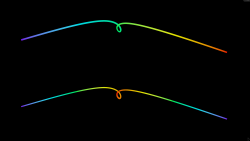
Measures point density within a certain radius.
// POINT WRANGLE
int samples = chi('samples');
float radius = chf('radius');
int pts[] = pcfind(0, 'P', v@P, radius, samples);
float dens = len(pts) / float(samples);
f@dens = dens;
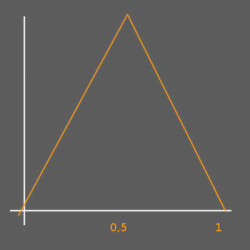
Parametric U on curve:
float u = vertexcurveparam(0, i@vtxnum);
Symmetrical U:
float us = 1.0 - abs(u - 0.5) * 2.0;

// vertex wrangle
string geo_uv = geounwrap(0, 'uv');
vector bb = relbbox(geo_uv, v@uv);
vector size = getbbox_size(geo_uv);
float aspect = size.y / size.x;
bb.y *= aspect;
v@uv = bb;
float u = v@P.x;
v@P.y = 1.0 - abs((abs(u) % (2.0)) - 1.0);

This will shorten and cubicly interpolate in-between point positions an open curve by a custom percentage.
float amount = chf('amount');
float u = vertexcurveparam(0, i@vtxnum);
float um = fit01(u, amount, 1.0 - amount);
vector uvw = set(um, 0.0, 0.0);
int pts[] = expandpointgroup(0, '*');
insert(pts, 0, 0);
append(pts, npoints(0)-1);
vector pos[];
foreach(int pt; pts){
vector pos_pt = point(0, 'P', pt);
append(pos, pos_pt);
}
v@P = spline('cubic', um, pos);
Detail wrangle. Optionally replace * with group name.
int pts[] = expandpointgroup(0, '*');
float values[] = {};
foreach(int pt; pts){
float val = point(0, 'val', pt);
append(values, val);
}
f@val_avg = avg(values);

Prepend a promote node from points to primitives for a random float value named h with the promotion method set to "Array of all". Next, add a point wrangle that sums slices of the array:
float h[] = prim(0, 'h', i@primnum);
float s = sum(h[0:i@ptnum+1]);
v@P.y = s;
// SHUFFLE POINTS
int seed = chi('seed');
int pts[] = expandpointgroup(0, 'ends');
float vals[];
resize(vals, len(pts));
foreach(int i; float v; vals){
vals[i] = rand(i, seed);
}
int idx[] = argsort(vals);
i[]@ends = reorder(pts, idx);